|
Reservados todos los derechos a: |
MULTIPLICACION DE RADICALESMultiplicación de radicales con el mismo índice [editar]Se multiplica los coeficientes entre sí y las cantidades subradicales entre sí, dando este último producto bajo el signo radical común y se simplifica el resultado. Ejemplo:
Otro ejemplo:
Multiplicación de radicales con diferente índice [editar]Ejemplo:
Primero, se determina el mínimo común múltiplo de los índices. Este será el índice de todos los radicales en la operación. En este caso el mínimo común múltiplo sería 20 ya que 4 · 5 = 20.
Si es posible, se realiza una extracción de factores, como en este caso:
|
|
 ·
·  =
= 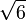
![sqrt[3]{x^3y^5}](http://upload.wikimedia.org/math/e/5/5/e553642612b0f853fcdcd57f19d30f84.png) ·
· ![sqrt[3]{x^2y^4}](http://upload.wikimedia.org/math/a/0/d/a0d91715e9a2ce294baf15a75a85ea93.png) =
= ![sqrt[3]{x^5y^9}](http://upload.wikimedia.org/math/0/9/b/09b928b9671b4273f88b761a36a0d5e6.png)
![sqrt[4]{x^2y^2}](http://upload.wikimedia.org/math/e/b/3/eb3bbd2889390c0697bc8a946de0b30d.png) ·
· ![sqrt[5]{x^3y}](http://upload.wikimedia.org/math/6/2/a/62a7aca3e68b81e410bc34935b4ab6ce.png)
![sqrt[20]{(x^2y^2)^5}](http://upload.wikimedia.org/math/3/9/6/3964f1677b145df53b3ef9b74a19816e.png) ·
· ![sqrt[20]{(x^3y)^4}](http://upload.wikimedia.org/math/5/8/e/58e1bbdbfa5d42b9385883a78b4810c0.png)
![sqrt[20]{x^{10}y^{10}}](http://upload.wikimedia.org/math/3/b/3/3b33a03097644cad4da0529a09eb7e7a.png) ·
· ![sqrt[20]{x^{12}y^4}](http://upload.wikimedia.org/math/e/0/a/e0a763ce251f2506f62f5a6bd9ae7854.png)
![sqrt[20]{x^{22}y^{14}}](http://upload.wikimedia.org/math/1/7/0/170f00d3f1c2eb6d2707e711a7f2a50e.png)
![xsqrt[20]{x^2y^{14}}](http://upload.wikimedia.org/math/1/b/5/1b553fef6814f16c7bfd46daeaa13ba3.png)